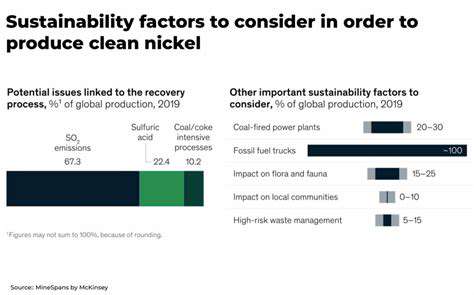
Classical Path Planning Algorithms
Dijkstra's Algorithm
When examining path planning techniques, Dijkstra's algorithm stands out as a foundational graph traversal method. Originally developed by Dutch computer scientist Edsger Dijkstra in 1956, this approach systematically finds the shortest path between a starting point and all other nodes in a network. What makes this algorithm particularly valuable is its guarantee of optimality - it will always find the shortest possible path when all edge weights are non-negative, which is typical in most navigation scenarios. Robots and autonomous systems frequently employ this method when operating in predictable environments with static obstacles.
From an implementation perspective, Dijkstra's approach works by continuously expanding the shortest path found thus far. It maintains a priority queue that selects the next node to explore based on accumulated distance. While remarkably reliable, the algorithm does face computational challenges in large-scale environments. The time complexity of O(E log V) means performance degrades significantly when dealing with extensive maps containing thousands of nodes and connections. Engineers must carefully consider these limitations when implementing the algorithm in memory-constrained systems.
A* Search Algorithm
Building upon Dijkstra's foundation, the A* algorithm introduces a game-changing optimization through heuristic estimation. Developed in 1968 at Stanford Research Institute, this method revolutionizes pathfinding by incorporating knowledge about the goal location. The heuristic function acts as a smart guide, estimating the remaining distance to the target and allowing the algorithm to prioritize more promising paths. This innovation often reduces the search space dramatically compared to blind search methods.
In practical applications, A* demonstrates particular strength in complex environments where conventional methods might struggle. The algorithm's dual consideration of actual path cost and estimated remaining distance creates an efficient balance between thoroughness and speed. Autonomous vehicles frequently rely on variations of A* for urban navigation, where numerous obstacles and dynamic conditions exist. Proper heuristic design is crucial - overly optimistic estimates can lead to suboptimal paths, while conservative ones may negate the algorithm's advantages.
Breadth-First Search (BFS)
For scenarios requiring exhaustive exploration, Breadth-First Search offers a straightforward yet powerful solution. This methodical approach examines all possible paths at the current depth before proceeding to deeper levels, making it ideal for uniform cost environments. Transportation systems often utilize BFS variants when calculating shortest routes where all path segments have equal weight.
The algorithm's queue-based implementation ensures systematic coverage of the search space, guaranteeing discovery of the shortest path (in terms of number of edges) if one exists. However, this comprehensive approach comes with memory limitations - BFS must store all nodes at the current depth level before proceeding. In wide but shallow graphs, this can lead to substantial memory consumption, making the algorithm less suitable for certain large-scale applications compared to more sophisticated methods.
Potential Field Methods
Taking inspiration from physics, potential field methods model navigation as movement through an energy landscape. The goal generates an attractive pull while obstacles create repulsive forces. This intuitive framework allows for real-time path adjustments, making it popular in reactive robotics applications. The elegance lies in its mathematical simplicity - the robot essentially follows the gradient of the combined potential field.
Despite its computational efficiency, practitioners must address several challenges. Local minima can trap robots in energy valleys where all immediate movements appear unfavorable. Various solutions exist, including random walks or virtual obstacles, but these add complexity. Potential fields work best in moderately complex environments where global optimality is less critical than real-time responsiveness.
Rapidly-exploring Random Trees (RRTs)
For high-dimensional planning problems, RRTs offer a probabilistic alternative to deterministic methods. Developed in the late 1990s, this algorithm constructs a search tree by randomly sampling the configuration space. This stochastic approach excels in complex environments where analytical solutions are impractical, such as robotic arm manipulation or spacecraft trajectory planning.
The random sampling nature allows RRTs to quickly explore vast spaces while avoiding explicit obstacle representation. Modern variants incorporate optimization techniques to refine the initially discovered paths. While not guaranteeing optimality, RRTs provide probabilistically complete solutions - given sufficient time, the probability of finding a valid path approaches certainty. This makes them indispensable for many real-world robotic applications.
Artificial Potential Field
This approach extends basic potential field concepts with additional refinements for practical implementation. By carefully designing the attractive and repulsive potential functions, engineers can create smooth navigation behaviors. The method's computational lightness enables deployment on resource-constrained platforms while maintaining adequate performance for many applications.
Challenges persist with oscillatory behaviors near obstacles and local minima traps. Various hybrid approaches combine potential fields with other methods to overcome these limitations. The technique remains popular for its intuitive physical analogy and real-time performance characteristics in moderately complex environments.
Advanced Path Planning Approaches
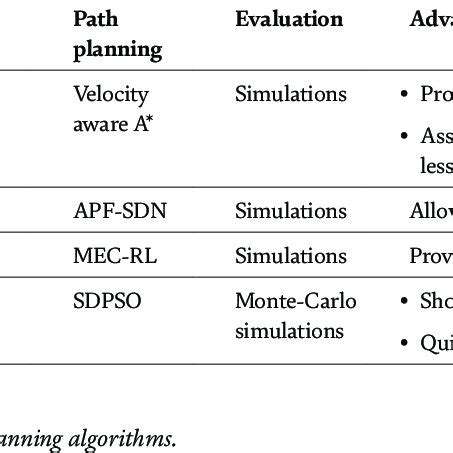
Hybrid A*
Bridging discrete and continuous planning, Hybrid A* merges grid-based efficiency with motion continuity considerations. Automotive systems particularly benefit from this approach when navigating parking lots or tight urban spaces. The algorithm's dual nature allows it to respect vehicle kinematics while maintaining search efficiency through discrete state representation.
By incorporating real-world constraints like turning radius and acceleration limits, Hybrid A* generates more physically plausible paths than pure grid-based methods. This makes it invaluable for autonomous vehicle applications where smooth, executable trajectories are essential. The additional computational cost is often justified by the improved path quality in complex maneuvering scenarios.
Informed Search Algorithms
Modern informed search techniques extend beyond basic A* with adaptive heuristics and learning components. These advanced variants can adjust their search strategy based on environmental characteristics or past experience. Machine learning integrations enable continuous heuristic improvement, potentially outperforming static heuristic designs after sufficient training.
The flexibility of informed search makes it adaptable to diverse scenarios, from video game pathfinding to logistics optimization. Recent developments incorporate multi-objective considerations, allowing trade-offs between path length, safety margins, energy consumption, and other factors. This versatility ensures informed search remains at the forefront of path planning research.
Enhanced Potential Field Methods
Contemporary potential field implementations address classical limitations through various enhancements. Harmonic potential fields guarantee absence of local minima, while vector field methods improve guidance in complex topologies. These refinements expand the applicability of potential-based approaches to more demanding environments without sacrificing real-time performance.
Combination with other techniques, such as using potential fields for local refinement of globally planned paths, creates robust hybrid systems. The continuing evolution of potential field methods demonstrates their enduring value in the path planning toolkit.
Graph-Based Optimization
Modern graph methods leverage advanced data structures and pre-processing to achieve remarkable efficiency gains. Techniques like contraction hierarchies or transit node routing enable extremely fast query times for large-scale problems. These optimizations are revolutionizing applications like global navigation systems and logistics networks.
The mathematical elegance of graph representations allows incorporation of diverse constraints and objectives. Recent work extends these methods to dynamic graphs where connections change over time, opening new possibilities for real-time adaptive planning.
Sampling-Based Advancements
State-of-the-art sampling methods combine the exploratory power of RRTs with optimization techniques. Algorithms like RRT* asymptotically approach optimality, while informed variants focus sampling in promising regions. These developments address the traditional limitation of random sampling methods regarding solution quality.
Parallel implementations harness modern computing architectures to explore complex spaces efficiently. The combination of sampling with machine learning for intelligent exploration points toward exciting future directions in high-dimensional planning.
Dynamic Dijkstra Variations
Contemporary adaptations of Dijkstra's algorithm handle dynamic environments where edge costs change over time. Incremental recomputation techniques and clever data structure usage maintain the algorithm's theoretical guarantees while improving practical performance. These variants prove invaluable for applications like traffic-aware routing or network load balancing.
The enduring relevance of Dijkstra's approach, sixty years after its invention, demonstrates the fundamental value of its core principles. Modern implementations often combine it with hierarchical decomposition or preprocessing to scale to enormous graphs.
Performance Evaluation and Optimization

Comprehensive Performance Metrics
Effective evaluation requires multi-dimensional assessment beyond simple path length or computation time. Modern metrics frameworks consider factors like smoothness, clearance from obstacles, energy efficiency, and computational resource usage. This holistic view ensures algorithms meet all practical requirements rather than optimizing single aspects at the expense of others.
Standardized benchmark environments facilitate objective comparison between methods. The robotics community has developed several challenging test scenarios that stress different algorithm capabilities. Careful metric selection and rigorous benchmarking are essential for meaningful performance evaluation in both research and industrial applications.
Algorithm Optimization Techniques
Optimization begins with profiling to identify true bottlenecks rather than assumed ones. Modern tools provide detailed insights into memory access patterns, cache behavior, and parallelization opportunities. Data structure selection often yields dramatic improvements - specialized priority queues or spatial indexing can transform algorithm performance.
Algorithmic optimizations should preserve theoretical guarantees while improving practical efficiency. Techniques like lazy evaluation or approximate computations can provide acceptable trade-offs in many real-world applications. The optimal approach depends heavily on specific use case requirements and constraints.
Evaluation Tool Ecosystem
The modern planner's toolkit includes sophisticated visualization systems, statistical analysis packages, and hardware-in-the-loop testing frameworks. Interactive debugging tools enable deep inspection of algorithm behavior at each decision point. Logging and replay capabilities support thorough post-analysis of complex planning scenarios.
Cloud-based evaluation platforms facilitate large-scale testing across diverse environments and conditions. These tools collectively enable comprehensive validation that catches subtle issues before deployment in critical applications.
Impact Quantification
Demonstrating optimization value requires rigorous before-after comparison under controlled conditions. Statistical significance testing ensures observed improvements aren't incidental. Real-world deployment metrics often reveal considerations absent from laboratory testing, highlighting the importance of field validation.
Long-term monitoring tracks performance degradation or improvement trends, informing future optimization priorities. Clear documentation of optimization processes and results creates institutional knowledge that benefits subsequent development cycles.